| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 1 Patterns in Mathematics
Welcome to this dedicated resource focusing on the solutions for the exercises within the inaugural chapter, "Patterns in Mathematics", featured in the latest Class 6 Ganita Prakash textbook published by NCERT for the academic year 2024-25. This solution guide is meticulously crafted to serve as a comprehensive companion for students navigating the fascinating world of mathematical patterns. It aims to provide clear, step-by-step assistance, ensuring that learners can confidently approach problems involving the identification, thorough analysis, logical extension, and even creation of diverse mathematical patterns presented in their textbook.
Students who find themselves challenged by the task of discerning the underlying rule or logic governing a sequence will find these solutions particularly beneficial. The exercises in "Patterns in Mathematics" explore various forms, and these solutions address them all systematically. The types of patterns encountered include:
- Numerical Sequences: Such as arithmetic progressions (e.g., $4, 9, 14, 19, ...$ where a constant value, $5$, is added) or geometric progressions (e.g., $2, 6, 18, 54, ...$ where each term is multiplied by a constant value, $3$).
- Visual and Geometric Patterns: Sequences involving shapes that might grow, shrink, rotate, or change in arrangement following a predictable logic.
- Repeating Patterns: Sequences of numbers, shapes, or symbols that cycle through a specific set order.
- Simple Algebraic Patterns: Introductory instances where a pattern can be described using a basic variable expression, like the sequence $3, 5, 7, 9, ...$ potentially being represented by a rule related to $2n+1$.
The core strength of this resource lies in its methodical approach. For numerical patterns, the solutions explicitly demonstrate how to determine the relationship between consecutive terms – calculating the constant difference (like $a_{n+1} - a_n$) in arithmetic sequences or the constant ratio (like $\frac{a_{n+1}}{a_n}$) in geometric ones. Once this fundamental rule is established, the solutions illustrate its application to predict subsequent terms or identify missing elements within a given sequence. When tackling visual or geometric patterns, the provided explanations carefully break down the transformation from one step to the next. Changes in critical attributes such as shape components, overall size, orientation, or the quantity of elements are highlighted, empowering students to accurately forecast the next figure or stage in the pattern's evolution.
Furthermore, these solutions guide students through problems requiring the formulation of a pattern's rule, expressed either descriptively in words or using introductory mathematical notation. By engaging with these detailed walkthroughs, students are expected to gain more than just the correct answers. The primary objective is to foster a deeper understanding of the logical reasoning and observational skills that are essential for mastering pattern recognition. This is not merely about solving Chapter 1 exercises; it's about building a foundational skill crucial for grasping more advanced concepts in algebra, geometry, and logical thinking encountered later in their mathematical education using the NCERT Class 6 Ganita Prakash (2024-25) syllabus. The emphasis is firmly placed on clarity and structured thinking, ensuring students grasp why a pattern functions as it does.
Figure it Out (Page 2)
Question 1. Can you think of other examples where mathematics helps us in our everyday lives?
Answer:
Yes, math helps us in many ways every single day! We use it without even thinking sometimes. Math is like a tool that helps us figure things out and understand the world around us.
Here are some examples:
1. Using Money: When you buy something at the store, you use math to count your money, make sure you get the right change back, and figure out if you have enough money for what you want to buy. You use it to save money or find discounts.
2. Cooking and Baking: Recipes tell you exactly how much flour or sugar to use. That's math! If you want to make a double batch of cookies, you use math to double all the ingredients.
3. Telling Time: Knowing what time it is, how long it takes to get somewhere, or how much time is left until your favorite show starts is all about using math with numbers on a clock or calendar.
4. Travelling: When you go somewhere new, you might look at a map and use math to figure out how far it is or how long the trip will take.
5. Making Things: If you're building something with LEGOs, drawing, or helping measure for a new carpet, you're using math to measure lengths and sizes so everything fits just right.
6. Staying Healthy: Doctors use math to figure out how much medicine someone needs. People who exercise might use math to count calories or steps.
7. Understanding Information: When you see charts or graphs that show how many students like different sports, that's math helping you understand information quickly.
8. Playing with Gadgets: Computers, phones, video games, and TVs all work because of math that is programmed inside them. Math is key to making technology work!
So, math is not just for school! It helps us do lots of important and fun things every day.
Question 2. How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Answer:
Math is super important for making our world better and helping people do amazing things. It's like the secret ingredient behind many inventions and discoveries!
In Science: Math helps scientists understand how the world works. They use math to measure things, do experiments, and figure out why things happen, like how fast a ball falls or how plants grow. Without math, it would be much harder to learn new things about space, animals, or anything else!
With Money and Countries: Math helps countries manage their money and plan for the future. It also helps us understand what people think, like when we count votes in an election. Math helps keep things fair and organized.
Building Things: Think about tall buildings, strong bridges, and even your house. Math helps engineers plan and build them safely. They use math to make sure everything is the right size and shape so it doesn't fall down!
Making Technology: All the cool gadgets we use, like phones, computers, and TVs, need math to work. Math is used to design their parts and write the instructions (called code) that tell them what to do. Even cars, trains, and planes are designed using lots of math!
Keeping Track of Time: Our calendars and clocks, which help us know the date and time, are based on math. Math helps us understand the movements of the sun and moon to make calendars and helps us divide time into seconds, minutes, and hours for clocks.
So, math isn't just numbers; it's a powerful tool that has helped people invent things, build big structures, explore the world, and understand how everything works. It helps us make life easier and better!
Figure it Out (Page 3)
| Table 1 Examples of number sequences | |
|---|---|
| 1, 1, 1, 1, 1, 1, 1, ... | (All 1’s) |
| 1, 2, 3, 4, 5, 6, 7, ... | (Counting numbers) |
| 1, 3, 5, 7, 9, 11, 13, ... | (Odd numbers) |
| 2, 4, 6, 8, 10, 12, 14, ... | (Even numbers) |
| 1, 3, 6, 10, 15, 21, 28, ... | (Triangular numbers) |
| 1, 4, 9, 16, 25, 36, 49, ... | (Squares) |
| 1, 8, 27, 64, 125, 216, ... | (Cubes) |
| 1, 2, 3, 5, 8, 13, 21, ... | (Virahānka numbers) |
| 1, 2, 4, 8, 16, 32, 64, ... | (Powers of 2) |
| 1, 3, 9, 27, 81, 243, 729, ... | (Powers of 3) |
Question 1. Can you recognize the pattern in each of the sequences in Table 1?
Answer:
Yes, we can find the pattern in each list of numbers in Table 1.
1. 1, 1, 1, 1, 1, 1, 1, ...
Pattern: The pattern is very simple! Every number in the list is the same, always 1.
$\checkmark$ Pattern Recognized.
2. 1, 2, 3, 4, 5, 6, 7, ...
Pattern: This is the list of counting numbers, starting from 1. Each number is just 1 more than the number before it.
$1 + 1 = 2$, $2 + 1 = 3$, and so on.
$\checkmark$ Pattern Recognized.
3. 1, 3, 5, 7, 9, 11, 13, ...
Pattern: This is the list of odd numbers. Each number is found by adding 2 to the number before it.
$1 + 2 = 3$, $3 + 2 = 5$, and so on.
$\checkmark$ Pattern Recognized.
4. 2, 4, 6, 8, 10, 12, 14, ...
Pattern: This is the list of even numbers. Each number is found by adding 2 to the number before it.
$2 + 2 = 4$, $4 + 2 = 6$, and so on.
$\checkmark$ Pattern Recognized.
5. 1, 3, 6, 10, 15, 21, 28, ...
Pattern: To get the next number, you add an increasing number each time. You add 2, then 3, then 4, then 5, and so on.
$1 + 2 = 3$, $3 + 3 = 6$, $6 + 4 = 10$, $10 + 5 = 15$, etc.
These are called triangular numbers.
$\checkmark$ Pattern Recognized.
6. 1, 4, 9, 16, 25, 36, 49, ...
Pattern: These are the square numbers. To get a number in the list, you take its position number (1st, 2nd, 3rd, etc.) and multiply it by itself.
1st number: $1 \times 1 = 1$
2nd number: $2 \times 2 = 4$
3rd number: $3 \times 3 = 9$
And so on.
$\checkmark$ Pattern Recognized.
7. 1, 8, 27, 64, 125, 216, ...
Pattern: These are the cube numbers. To get a number in the list, you take its position number (1st, 2nd, 3rd, etc.) and multiply it by itself three times.
1st number: $1 \times 1 \times 1 = 1$
2nd number: $2 \times 2 \times 2 = 8$
3rd number: $3 \times 3 \times 3 = 27$
And so on.
$\checkmark$ Pattern Recognized.
8. 1, 2, 3, 5, 8, 13, 21, ...
Pattern: Starting from the third number, each number is the sum of the two numbers right before it.
$1 + 2 = 3$
$2 + 3 = 5$
$3 + 5 = 8$
And so on. These are called Virahānka numbers (like Fibonacci numbers).
$\checkmark$ Pattern Recognized.
9. 1, 2, 4, 8, 16, 32, 64, ...
Pattern: To get the next number, you multiply the number before it by 2.
$1 \times 2 = 2$
$2 \times 2 = 4$
$4 \times 2 = 8$
And so on. These are called powers of 2.
$\checkmark$ Pattern Recognized.
10. 1, 3, 9, 27, 81, 243, 729, ...
Pattern: To get the next number, you multiply the number before it by 3.
$1 \times 3 = 3$
$3 \times 3 = 9$
$9 \times 3 = 27$
And so on. These are called powers of 3.
$\checkmark$ Pattern Recognized.
Question 2. Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.
Answer:
Here are the lists of numbers with the next three numbers added, and the rule explained in simple words:
1. Sequence: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
Rule: The rule is simple: the number is always 1. It never changes.
2. Sequence: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Rule: Start at 1 and add 1 each time to get the next number. (These are the counting numbers).
3. Sequence: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Rule: Start at 1 and add 2 each time to get the next number. (These are the odd numbers).
Next numbers: $13+2 = 15$, $15+2 = 17$, $17+2 = 19$.
4. Sequence: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
Rule: Start at 2 and add 2 each time to get the next number. (These are the even numbers).
Next numbers: $14+2 = 16$, $16+2 = 18$, $18+2 = 20$.
5. Sequence: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55
Rule: Add a number to the last term, but the number you add goes up by 1 each time: add 2, then add 3, then add 4, and so on.
Next numbers: $28 + 8 = 36$, $36 + 9 = 45$, $45 + 10 = 55$.
6. Sequence: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Rule: Multiply the position number of the term by itself. (1st term: $1 \times 1$; 2nd term: $2 \times 2$; etc.).
Next numbers: 8th term is $8 \times 8 = 64$, 9th term is $9 \times 9 = 81$, 10th term is $10 \times 10 = 100$.
7. Sequence: 1, 8, 27, 64, 125, 216, 343, 512, 729
Rule: Multiply the position number of the term by itself three times. (1st term: $1 \times 1 \times 1$; 2nd term: $2 \times 2 \times 2$; etc.).
Next numbers: 7th term is $7 \times 7 \times 7 = 343$, 8th term is $8 \times 8 \times 8 = 512$, 9th term is $9 \times 9 \times 9 = 729$.
8. Sequence: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
Rule: Start with 1 and 2. From the third number onwards, add the two numbers that came just before it.
Next numbers: $13 + 21 = 34$, $21 + 34 = 55$, $34 + 55 = 89$.
9. Sequence: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512
Rule: Start at 1 and multiply by 2 each time to get the next number.
Next numbers: $64 \times 2 = 128$, $128 \times 2 = 256$, $256 \times 2 = 512$.
10. Sequence: 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683
Rule: Start at 1 and multiply by 3 each time to get the next number.
Next numbers: $729 \times 3 = 2187$, $2187 \times 3 = 6561$, $6561 \times 3 = 19683$.
Figure it Out (Page 5 - 6)
| Table 2 Pictorial representation of some number sequences | |
|---|---|
.jpg)
|
(All 1’s) |
.jpg)
|
(Counting numbers) |
.jpg)
|
(Odd numbers) |
.jpg)
|
(Even numbers) |
.jpg)
|
(Triangular numbers) |
.jpg)
|
(Squares) |
.jpg)
|
(Cubes) |
Question 1. Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence!
Answer:
| Next Picture (6th term) in Each Sequence | |
|---|---|
$\begin{matrix} \bullet \end{matrix}$ |
(All 1’s) |
$\begin{matrix} \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet \end{matrix}$ |
(Counting numbers) |
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$ |
(Odd numbers) |
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$ |
(Even numbers) |

|
(Triangular numbers) |
|
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$ |
(Squares) |
|
(Cubes) |
Below is the description of each sequence and how to draw the next picture (the 6th term):
1. Sequence: All 1's
Pattern: Each picture represents the number 1. The sequence is $1, 1, 1, 1, 1, 1, \dots$ The last picture shown in the table is the 5th term, which is 1.
How to draw the next picture: The next picture (the 6th term) is simply the representation of the number 1. Draw just one dot or object.
2. Sequence: Counting numbers
Pattern: The pictures represent the counting numbers $1, 2, 3, 4, 5, 6, \dots$ Each picture has one more dot than the previous one. The last picture shown in the table is the 5th term, which is 5 dots.
How to draw the next picture: The next number in the sequence is the 6th term, which is 6. Draw a group of 6 dots. You can arrange them in a way that continues the pattern shown in the table (e.g., two rows of three dots).
3. Sequence: Odd numbers
Pattern: The pictures represent the odd numbers $1, 3, 5, 7, 9, 11, \dots$ Each picture has two more dots than the previous one ($1+2=3$, $3+2=5$, $5+2=7$, $7+2=9$). The last picture shown in the table is the 5th term, which is 9 dots.
How to draw the next picture: The next number in the sequence is the 6th term, $9+2=11$. Take the picture for 9 dots and add 2 more dots to it, maintaining the arrangement style shown in the pattern.
4. Sequence: Even numbers
Pattern: The pictures represent the even numbers $2, 4, 6, 8, 10, 12, \dots$ Each picture has two more dots than the previous one ($2+2=4$, $4+2=6$, $6+2=8$, $8+2=10$). The last picture shown in the table is the 5th term, which is 10 dots.
How to draw the next picture: The next number in the sequence is the 6th term, $10+2=12$. Take the picture for 10 dots and add 2 more dots to it, following the arrangement shown in the pattern.
5. Sequence: Triangular numbers
Pattern: The pictures form triangles. The sequence is $1, 3, 6, 10, 15, 21, \dots$ The $n$-th triangular number is obtained by adding $n$ dots to the previous term. The 1st term is 1. The 2nd term is $1+2=3$. The 3rd term is $3+3=6$. The 4th term is $6+4=10$. The 5th term is $10+5=15$. The last picture shown in the table is the 5th term (15 dots).
How to draw the next picture: The next number is the 6th triangular number, which is $15 + 6 = 21$. Draw a triangle of dots with 6 rows. The rows will have $1, 2, 3, 4, 5,$ and $6$ dots from top to bottom.
6. Sequence: Squares
Pattern: The pictures form squares. The sequence is $1, 4, 9, 16, 25, 36, \dots$ The $n$-th square number is $n \times n$. The 1st term is $1 \times 1=1$. The 2nd term is $2 \times 2=4$. The 3rd term is $3 \times 3=9$. The 4th term is $4 \times 4=16$. The 5th term is $5 \times 5=25$. The last picture shown in the table is the 5th term (25 dots, a $5 \times 5$ square).
How to draw the next picture: The next number is the 6th square number, which is $6 \times 6 = 36$. Draw a $6 \times 6$ square grid of dots.
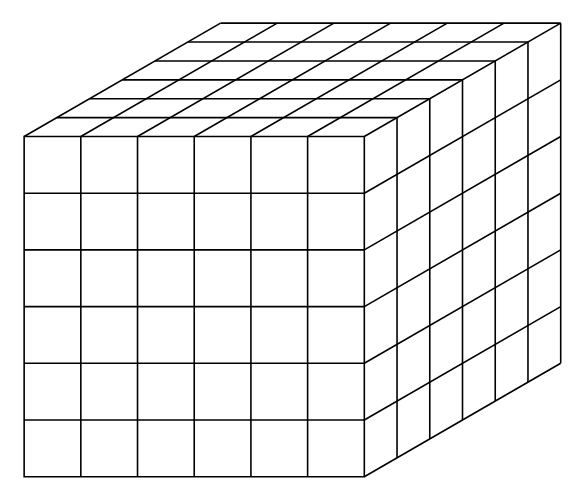
7. Sequence: Cubes
Pattern: The pictures represent cubes in 3 dimensions (or views of them). The sequence is $1, 8, 27, 64, 125, 216, \dots$ The $n$-th cube number is $n \times n \times n$. The 1st term is $1^3=1$. The 2nd term is $2^3=8$. The 3rd term is $3^3=27$. The 4th term is $4^3=64$. The 5th term is $5^3=125$. The last picture shown in the table is the 5th term (125 dots, a $5 \times 5 \times 5$ cube).
How to draw the next picture: The next number is the 6th cube number, which is $6 \times 6 \times 6 = 216$. Draw a picture that looks like a $6 \times 6 \times 6$ cube made of dots or blocks.
Question 2. Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers or squares? Why are 1, 8, 27, 64, 125, … called cubes?
This shows that the same number can be represented differently, and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Answer:
The names of these number lists come from the shapes you can make by arranging that many dots or objects.
The numbers 1, 3, 6, 10, 15, ... are called triangular numbers because you can arrange this many dots to form triangles. The first one (1) is a dot (a small triangle). The second (3) makes a triangle with 2 rows ($1+2$). The third (6) makes a triangle with 3 rows ($1+2+3$), and so on. Each number is the sum of counting numbers up to a certain point, and this shape looks like a filled triangle.
The numbers 1, 4, 9, 16, 25, ... are called square numbers because you can arrange this many dots to form square shapes. The first one (1) makes a $1 \times 1$ square. The second (4) makes a $2 \times 2$ square. The third (9) makes a $3 \times 3$ square, and so on. You get these numbers by multiplying a counting number by itself (like $1 \times 1 = 1$, $2 \times 2 = 4$, $3 \times 3 = 9$, etc.).
The numbers 1, 8, 27, 64, 125, ... are called cubes because you can arrange this many small blocks or dots to form solid cube shapes in 3 dimensions. The first one (1) is a $1 \times 1 \times 1$ cube. The second (8) is a $2 \times 2 \times 2$ cube. The third (27) is a $3 \times 3 \times 3$ cube, and so on. You get these numbers by multiplying a counting number by itself three times (like $1 \times 1 \times 1 = 1$, $2 \times 2 \times 2 = 8$, $3 \times 3 \times 3 = 27$, etc.).
Yes, the same number can be shown in different ways pictorially, depending on what we want to show about it.
Let's try representing the number 6 in different ways:
-
As a single group (showing the total count):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
This just shows the number 6 itself.
-
As a rectangle (showing it can be made by multiplying):
$\begin{matrix} \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet \end{matrix}$
This shows that 6 can be made by arranging dots in 2 rows with 3 dots in each row ($2 \times 3 = 6$).
-
As another rectangle:
$\begin{matrix} \bullet & \bullet \\ \bullet & \bullet \\ \bullet & \bullet \end{matrix}$
This shows that 6 can also be made by arranging dots in 3 rows with 2 dots in each row ($3 \times 2 = 6$).
-
As a triangle (showing it is a triangular number):
$\begin{matrix} & & \bullet & & \\ & \bullet & & \bullet & \\ \bullet & & \bullet & & \bullet \end{matrix}$
or
$\begin{matrix} \bullet \\ \bullet & \bullet \\ \bullet & \bullet & \bullet \end{matrix}$
This shows that 6 dots can form a triangle with 3 rows, which is why 6 is a triangular number ($1+2+3=6$).
Let's try representing the number 12 in different ways:
-
As a single group (showing the total count):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
This just shows the number 12 itself.
-
As a rectangle (showing it can be made by multiplying):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \end{matrix}$
This shows that 12 can be made by arranging dots in 3 rows with 4 dots in each row ($3 \times 4 = 12$).
-
As another rectangle:
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
This shows that 12 can also be made by arranging dots in 2 rows with 6 dots in each row ($2 \times 6 = 12$).
These examples show how the way we arrange dots can highlight different properties or factors of a number, giving it different "roles".
Question 3. You will have noticed that 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and in a square. Make pictures in your notebook illustrating this!
This shows that the same number can be represented differently, and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Answer:
Yes, the number 36 is indeed special because you can arrange 36 dots to make both a triangle and a square shape perfectly. Let's see how:
Why 36 is a Triangular Number:
Triangular numbers are formed by arranging dots in the shape of a triangle, with each new row having one more dot than the row above it. The numbers are $1, 3, 6, 10, 15, 21, 28, 36, \dots$ They are the sums of consecutive counting numbers:
$1 = 1$
$3 = 1 + 2$
$6 = 1 + 2 + 3$
$10 = 1 + 2 + 3 + 4$
...and so on.
To get 36, you add the first 8 counting numbers:
$1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36$
... (i)
Because the sum of the first 8 counting numbers is 36, it means 36 dots can be arranged to form a triangle with 8 rows. The top row has 1 dot, the next has 2, the next has 3, and so on, until the bottom row has 8 dots.
Here is the picture using dots:
$\begin{matrix} &&&&&&&& \bullet &&&&&&&& \\ &&&&&&& \bullet & & \bullet &&&&&&& \\ &&&&&& \bullet & & \bullet & & \bullet &&&&&& \\ &&&&& \bullet & & \bullet & & \bullet & & \bullet &&&&& \\ &&&& \bullet & & \bullet & & \bullet & & \bullet & & \bullet &&&& \\ &&& \bullet & & \bullet & & \bullet & & \bullet & & \bullet & & \bullet &&& \\ && \bullet & & \bullet & & \bullet & & \bullet & & \bullet & & \bullet & & \bullet && \\ & \bullet & & \bullet & & \bullet & & \bullet & & \bullet & & \bullet & & \bullet & & \bullet & \end{matrix}$
or, perhaps more clearly arranging rows:
$\begin{matrix} \bullet \\ \bullet & \bullet \\ \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
Why 36 is a Square Number:
Square numbers are formed by arranging dots in the shape of a square. The numbers are $1, 4, 9, 16, 25, 36, \dots$ They are obtained by multiplying a counting number by itself:
$1 = 1 \times 1$
$4 = 2 \times 2$
$9 = 3 \times 3$
...and so on.
To get 36, you multiply 6 by itself:
$6 \times 6 = 36$
... (ii)
Because $6 \times 6$ equals 36, it means 36 dots can be arranged to form a perfect square that is 6 dots wide and 6 dots tall (a $6 \times 6$ grid).
Here is the picture using dots:
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
Same Number, Different Pictures:
So, 36 dots can be arranged to make both a triangle and a square! This clearly shows that the same number (36) can be represented pictorially in different ways, which helps us see different properties or roles it can play in number patterns and shapes.
Representing Other Numbers Differently:
We can show other numbers in different picture ways too!
- A number like 12 can be shown as a line of 12 dots (a $1 \times 12$ rectangle):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
Or as a rectangle with 2 rows of 6 dots (a $2 \times 6$ rectangle):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
Or as a rectangle with 3 rows of 4 dots (a $3 \times 4$ rectangle):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \end{matrix}$
Each picture shows a different pair of numbers that multiply to make 12 ($1 \times 12$, $2 \times 6$, $3 \times 4$).
- An even number like 10 can always be shown as 2 rows of dots ($2 \times 5$ rectangle):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
showing it can be divided into two equal groups.
- A prime number like 7 can only be shown nicely as a line of 7 dots ($1 \times 7$):
$\begin{matrix} \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \end{matrix}$
You can't make a rectangle with more than one row unless it's just one long row, because prime numbers only have 1 and themselves as factors (numbers that divide them exactly).
These examples show how using pictures can help us understand different things about numbers, like what factors they have or what kind of number pattern they belong to.
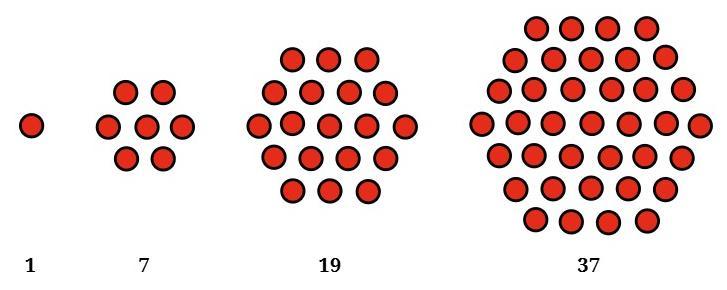
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Answer:
Looking at the pictures provided, the sequence of numbers represented by the dots is 1, 6, 15, 28, ...
As the question states, these numbers are called hexagonal numbers because the dots are arranged to form shapes of hexagons.
Drawing the Pictures (Hexagonal Numbers):
Here are the pictures for the first four hexagonal numbers using dots:
1 (1st Hexagonal Number):
$\begin{matrix} \bullet \end{matrix}$
This is like a hexagon with a "side length" of 1 dot.
6 (2nd Hexagonal Number):
$\begin{matrix} & \bullet & \bullet & \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ & \bullet & \bullet & \end{matrix}$
This forms a hexagon outline with 2 dots along each side (counting the corner dots shared between sides). It has a "side length" of 2.
15 (3rd Hexagonal Number):
$\begin{matrix} & & \bullet & \bullet & \bullet & & \\ & \bullet & \bullet & \bullet & \bullet & \bullet & \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ & \bullet & \bullet & \bullet & \bullet & \bullet & \\ & & \bullet & \bullet & \bullet & & \end{matrix}$
This forms a hexagon outline with 3 dots along each side. It has a "side length" of 3.
28 (4th Hexagonal Number):
$\begin{matrix} & & & \bullet & \bullet & \bullet & \bullet & & & \\ & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & & \\ & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \\ \bullet & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \\ & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & & \\ & & & \bullet & \bullet & \bullet & \bullet & & & \end{matrix}$
This forms a hexagon outline with 4 dots along each side. It has a "side length" of 4.
Finding the Next Number in the Sequence:
Let's look at how many dots are added to get from one picture to the next:
- From 1 to 6, we added $6 - 1 = 5$ dots.
- From 6 to 15, we added $15 - 6 = 9$ dots.
- From 15 to 28, we added $28 - 15 = 13$ dots.
The numbers being added are 5, 9, 13, ...
Now let's look at the pattern of these added numbers:
- From 5 to 9, the increase is $9 - 5 = 4$.
- From 9 to 13, the increase is $13 - 9 = 4$.
So, the numbers being added are increasing by 4 each time.
To find the next number to add after 13, we add 4:
$13 + 4 = 17$
Now, to find the next number in the original hexagonal sequence (after 28), we add this new number (17) to the last number (28):
$28 + 17 = 45$
The next number in the sequence 1, 6, 15, 28, ... is 45.
Drawing the Next Picture (The picture for 45):
The pictures have a "side length" that is the same as which term it is in the sequence. The 1st term (1) has side length 1. The 2nd term (6) has side length 2. The 3rd term (15) has side length 3. The 4th term (28) has side length 4.
Since 45 is the 5th term in the sequence, its picture will be a hexagon outline with a "side length" of 5 dots along each side. This means drawing a hexagon shape where each of the 6 outer edges has exactly 5 dots, including the corner dots.
Here is the picture using dots:
$\begin{matrix} & & & & \bullet & \bullet & \bullet & \bullet & \bullet & & & & \\ & & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & & & \\ & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & & \\ & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet \\ & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \\ & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & & \\ & & & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & \bullet & & & \\ & & & & \bullet & \bullet & \bullet & \bullet & \bullet & & & & \end{matrix}$
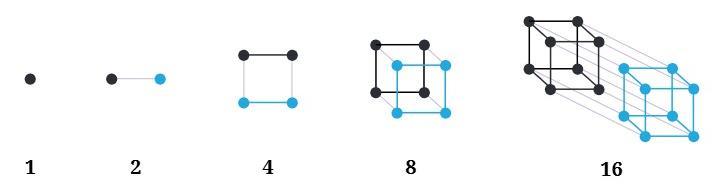
Here is one possible way of thinking about Powers of 2:
Answer:
Yes, we can draw pictures to show the sequences of Powers of 2 and Powers of 3. This helps us see how the numbers grow quickly!
Pictures for Powers of 2 (1, 2, 4, 8, 16, ...):
The example picture shows a good way. It starts with 1 thing, then shows that quantity doubling each time.
- Show 1 dot (for $2^0 = 1$).
- Show 2 dots (for $2^1 = 2$).
- Show 4 dots (for $2^2 = 4$).
- Show 8 dots (for $2^3 = 8$).
- Show 16 dots (for $2^4 = 16$), and so on.
You can arrange them to show the doubling clearly. Start with 1, then show two groups of 1 (total 2), then two groups of 2 (total 4), two groups of 4 (total 8), and so on. Each step is simply doubling the previous step.
Another way is using shapes and their areas: Start with a small $1 \times 1$ square (Area 1, for $2^0$). Then a $1 \times 2$ rectangle (Area 2, for $2^1$). Then a $2 \times 2$ square (Area 4, for $2^2$). Then a $2 \times 4$ rectangle (Area 8, for $2^3$). Then a $4 \times 4$ square (Area 16, for $2^4$). The area of the shape doubles at each step.
Pictures for Powers of 3 (1, 3, 9, 27, 81, ...):
For Powers of 3, we need pictures where the quantity triples each time. Each step is three times the step before.
Here is one possible way using dots:
- Show 1 dot (for $3^0 = 1$).
- Show 3 dots (for $3^1 = 3$). You could show them as three separate dots or three dots in a row.
- Show 9 dots (for $3^2 = 9$). You could show three groups of 3 dots, or arrange them nicely in a $3 \times 3$ square.
- Show 27 dots (for $3^3 = 27$). You could show three groups of 9 dots, or arrange them in a $3 \times 9$ rectangle. If you think in 3D, you could imagine a $3 \times 3 \times 3$ cube.
- Show 81 dots (for $3^4 = 81$). You could show three groups of 27 dots, or arrange them in a $9 \times 9$ square.
Another way is similar to the grouping method for Powers of 2, but this time we triple the groups:
- 1 dot (for $3^0 = 1$)
- Three groups of 1 dot (total 3, for $3^1 = 3$)
- Three groups of 3 dots (total 9, for $3^2 = 9$)
- Three groups of 9 dots (total 27, for $3^3 = 27$), and so on.
These pictures help us understand how powers work by showing the multiplication at each step visually!
Intext Questions (Page 7)
Adding Odd Numbers: Consider adding the first few odd numbers:
1 = 1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 + 5 + 7 + 9 + 11 = 36
It appears that the sum of the first n odd numbers is equal to n2 , a perfect square.

Question 1: By drawing a similar picture, can you say what is the sum of the first 10 odd numbers?
Answer:
Based on the pattern shown by adding the first few odd numbers, we see that the sum is always a perfect square.
The pattern is: Sum of the first $n$ odd numbers is equal to $n^2$.
We want to find the sum of the first 10 odd numbers.
Here, the number of odd numbers we are adding is $n = 10$.
Using the pattern, the sum of the first 10 odd numbers is $10^2$.
Calculation:
$10^2 = 10 \times 10 = 100$
So, the sum of the first 10 odd numbers is 100.
Drawing a similar picture:
The picture for the sum of the first 10 odd numbers would be a square grid with 10 rows and 10 columns. This grid would have a total of $10 \times 10 = 100$ dots.
You can imagine building this square step-by-step by adding the odd numbers:
- $1$: A $1 \times 1$ square (1 dot).
- $1 + 3$: Add 3 dots in an L-shape to make a $2 \times 2$ square (4 dots total).
- $1 + 3 + 5$: Add 5 dots in an L-shape to make a $3 \times 3$ square (9 dots total).
- ...
- Continue adding L-shapes of 7, 9, 11, 13, 15, 17, and finally 19 dots. Adding the 19 dots (the 10th odd number) will complete the $10 \times 10$ square.
The picture would be a filled square grid of 100 dots, showing the sum $1+3+5+...+19 = 100$.
Question 2: Now by imagining a similar picture, or by drawing it partially, as needed, can you say what is the sum of the first 100 odd numbers?
Answer:
From the previous examples and the pattern, we know that the sum of the first $n$ odd numbers is equal to $n^2$.
We want to find the sum of the first 100 odd numbers.
In this case, the number of odd numbers we are adding is $n = 100$.
Using the pattern, the sum of the first 100 odd numbers is $100^2$.
Let's calculate $100^2$:
$100^2 = 100 \times 100$
$100 \times 100 = 10000$
Therefore, the sum of the first 100 odd numbers is 10000.
Imagining the picture for this sum means thinking about a very large square grid. The sum of the first 100 odd numbers corresponds to the total number of dots in a square that is 100 dots wide and 100 dots tall. Such a grid would have $100 \times 100 = 10000$ dots in total. This helps us see why the sum is so large and confirms the pattern.
Intext Questions (Page 8)
Adding up and down: Let’s examine another interesting sequence that leads to square numbers:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Here, we are adding the numbers in a symmetrical fashion—first increasing, then decreasing. The total sum still results in a square number.

Answer:
Yes, we can definitely find a pictorial explanation for why adding numbers like $1$, $1+2+1$, $1+2+3+2+1$, and so on, gives us square numbers.
The pattern here is that we add numbers going up to a certain number (let's call it $n$) and then come back down to 1. The sum is $1 + 2 + 3 + ... + n + ... + 3 + 2 + 1$.
The result of this sum is always the square of the largest number in the sequence, which is $\mathbf{n^2}$.
Let's look at how the picture shows this:
- For $n=1$: The sum is just $1$. The picture is just 1 dot, which is a $1 \times 1$ square ($1^2$).
- For $n=2$: The sum is $1 + 2 + 1 = 4$. The picture can show 1 dot, then a row of 2 dots, then a row of 1 dot. When arranged cleverly, these 4 dots form a $2 \times 2$ square ($2^2$). You can see this in the diagram provided for $n=2$ (though only $n=3$ and $n=4$ examples are fully shown in the image).
- For $n=3$: The sum is $1 + 2 + 3 + 2 + 1 = 9$. The picture shows dots arranged in rows of 1, 2, 3, 2, and 1. When you put these rows together as shown in the image, they fit perfectly to make a $3 \times 3$ square. The total number of dots is 9, which is $3^2$.
- For $n=4$: The sum is $1 + 2 + 3 + 4 + 3 + 2 + 1 = 16$. The picture shows rows of 1, 2, 3, 4, 3, 2, and 1 dots arranged to form a $4 \times 4$ square. The total number of dots is 16, which is $4^2$.
So, the picture helps us see that the collection of dots from the sequence $1, 2, ..., n, ..., 2, 1$ can always be arranged to fill an $n \times n$ square. This visually proves that the sum is equal to $n^2$. The largest number $n$ tells us the size of the square.
Figure it Out (Page 8 - 9)
Question 1. Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, gives square numbers?
Answer:
Yes, there is a clear pictorial explanation for why the sum of counting numbers that increase up to $n$ and then decrease back to 1 (e.g., $1+2+...+n+...+2+1$) always results in a square number, specifically $n^2$.
Consider the structure of the sum for a peak number $n$:
$1 + 2 + 3 + ... + (n-1) + n + (n-1) + ... + 3 + 2 + 1$
This sequence of numbers corresponds to the number of dots in successive rows if we arrange them in a specific way, often forming a diamond or pyramid shape that can then be rearranged into a square.
Let's look at the first few examples pictorially (as shown in the diagram in the previous prompt, which is not included here but describes the concept):
- For $n=1$: The sum is 1. This is simply 1 dot, which forms a $1 \times 1$ square. The sum is $1^2$.
- For $n=2$: The sum is $1 + 2 + 1 = 4$. We can arrange these dots in rows of 1, then 2, then 1. If you place the row of 2 dots, and then place the row of 1 dot above and the other row of 1 dot below (or beside), they perfectly fit together to form a $2 \times 2$ square containing 4 dots. The sum is $2^2$.
- For $n=3$: The sum is $1 + 2 + 3 + 2 + 1 = 9$. We have rows of 1, 2, 3, 2, 1 dots. If you take the middle row of 3 dots and stack the other rows around it – the two rows of 2 dots and the two rows of 1 dot – they can be arranged to form a perfect $3 \times 3$ square containing 9 dots. The sum is $3^2$.
- For $n=4$: The sum is $1 + 2 + 3 + 4 + 3 + 2 + 1 = 16$. With rows of 1, 2, 3, 4, 3, 2, 1 dots, we can arrange these around the central row of 4 dots to form a $4 \times 4$ square containing 16 dots. The sum is $4^2$.
In general, when you take the numbers $1, 2, ..., n, ..., 2, 1$ as the lengths of rows of dots and arrange them symmetrically (for example, with the row of length $n$ in the middle, and the rows of length $n-1$ on either side, then $n-2$, and so on), the total shape formed is an $\mathbf{n \times n}$ square. The total number of dots is the area of this square, which is $n \times n = n^2$. This visual arrangement provides a compelling reason why the sum of this particular sequence of numbers equals a square number.
Question 2. By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be tha value of 1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1?
Answer:
The sequence of sums $1$, $1+2+1$, $1+2+3+2+1$, etc., follows the pattern where the sum of numbers increasing up to $n$ and decreasing back to 1 is equal to $n^2$.
The given sum is $1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1$.
In this sequence, the peak number (the largest number reached before decreasing) is 100.
According to the pattern, the sum is the square of the peak number, which is $n^2$ where $n = 100$.
Therefore, the value of the sum is $100^2$.
Calculation:
$100^2 = 100 \times 100 = 10000$
By imagining the pictorial representation, this sum corresponds to the total number of dots in a $100 \times 100$ square grid. The number of dots in such a grid is $100 \times 100 = 10000$.
The value of $1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1$ is 10000.
Question 3. Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?
Answer:
Let the "All 1's" sequence be denoted by $a_n = 1$ for $n = 1, 2, 3, \dots$. The sequence is 1, 1, 1, 1, ...
Part 1: Adding the All 1’s sequence up
Adding the sequence up means finding the cumulative sum of the terms. Let $S_n$ be the sum of the first $n$ terms of the sequence.
The first term is 1.
Sum of the first 2 terms: $1 + 1 = 2$.
Sum of the first 3 terms: $1 + 1 + 1 = 3$.
Sum of the first 4 terms: $1 + 1 + 1 + 1 = 4$.
In general, the sum of the first $n$ terms is $1 \times n = n$.
The sequence of sums is 1, 2, 3, 4, 5, 6, ...
This is the sequence of counting numbers (or natural numbers).
Part 2: Adding the All 1’s sequence up and down
The previous "adding up and down" pattern was $1$, $1+2+1$, $1+2+3+2+1$, etc., where the number of terms increased based on a peak number $n$. Applying this structure to the "All 1's" sequence means taking a symmetrical number of terms centered around a "peak" term (which is always 1). The number of terms in the sums are $1, 1+1+1=3, 1+1+1+1+1=5$, etc., which are the odd numbers.
Let's form sums using an increasing sequence of odd numbers of terms from the "All 1's" sequence.
Sum using 1 term: $a_1 = 1$. Sum = 1.
Sum using the first 3 terms ($a_1, a_2, a_3$): $1 + 1 + 1 = 3$.
Sum using the first 5 terms ($a_1, ..., a_5$): $1 + 1 + 1 + 1 + 1 = 5$.
Sum using the first 7 terms ($a_1, ..., a_7$): $1 + 1 + 1 + 1 + 1 + 1 + 1 = 7$.
The sum using the first $2k-1$ terms (the $k$-th odd number of terms) from the "All 1's" sequence will be $(2k-1) \times 1 = 2k-1$.
The sequence of sums is 1, 3, 5, 7, 9, 11, ...
This is the sequence of odd numbers.
Question 4. Which sequence do you get when you start to add the Counting numbers up? Can you give a smaller pictorial explanation?
Answer:
The sequence of Counting numbers is 1, 2, 3, 4, 5, ...
When we start to add the Counting numbers up, we are calculating the cumulative sum at each step:
- Sum of the first 1 counting number: $1 = 1$
- Sum of the first 2 counting numbers: $1 + 2 = 3$
- Sum of the first 3 counting numbers: $1 + 2 + 3 = 6$
- Sum of the first 4 counting numbers: $1 + 2 + 3 + 4 = 10$
- Sum of the first 5 counting numbers: $1 + 2 + 3 + 4 + 5 = 15$
- Sum of the first 6 counting numbers: $1 + 2 + 3 + 4 + 5 + 6 = 21$
- ... and so on.
The sequence we get by adding the Counting numbers up is 1, 3, 6, 10, 15, 21, ...
This sequence is known as the sequence of triangular numbers.
Pictorial Explanation:
We can visualize this by arranging dots to form triangles.
- The first term is 1. Picture: A single dot. This is a triangle with 1 row.
- The second term is 3 ($1+2$). Picture: Arrange 1 dot on top of 2 dots. This forms a triangle with 2 rows.
- The third term is 6 ($1+2+3$). Picture: Arrange 1 dot on top of 2 dots, on top of 3 dots. This forms a triangle with 3 rows.
- The fourth term is 10 ($1+2+3+4$). Picture: Arrange 1 dot on top of 2 dots, on top of 3 dots, on top of 4 dots. This forms a triangle with 4 rows.
Each picture representing the sum of the first $n$ counting numbers is a triangle with $n$ rows, where the number of dots in each row increases by one from top to bottom (or bottom to top). The total number of dots in the triangle is the sum $1 + 2 + ... + n$. This visual representation clearly shows why adding counting numbers up results in the sequence of triangular numbers.
Question 5. What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, … ? Which sequence do you get? Why? Can you explain it with a picture?
Answer:
Let's add the consecutive pairs of triangular numbers as requested.
The sequence of triangular numbers is 1, 3, 6, 10, 15, 21, 28, 36, ...
Adding consecutive pairs:
- $1 + 3 = 4$
- $3 + 6 = 9$
- $6 + 10 = 16$
- $10 + 15 = 25$
- $15 + 21 = 36$
- ...and so on.
The sequence we get is 4, 9, 16, 25, 36, ...
This sequence is the sequence of square numbers (specifically, the squares starting from $2^2$).
$4 = 2^2$
$9 = 3^2$
$16 = 4^2$
$25 = 5^2$
$36 = 6^2$
Why this happens:
The $n$-th triangular number, denoted as $T_n$, is the sum of the first $n$ natural numbers, $T_n = 1 + 2 + ... + n$. The formula for $T_n$ is $\frac{n(n+1)}{2}$.
We are adding consecutive triangular numbers, which means we are looking at the sum of the $n$-th triangular number and the $(n+1)$-th triangular number, i.e., $T_n + T_{n+1}$.
$T_n = \frac{n(n+1)}{2}$
$T_{n+1} = \frac{(n+1)((n+1)+1)}{2} = \frac{(n+1)(n+2)}{2}$
Let's add them:
$T_n + T_{n+1} = \frac{n(n+1)}{2} + \frac{(n+1)(n+2)}{2}$
Combine the fractions with a common denominator:
$= \frac{n(n+1) + (n+1)(n+2)}{2}$
Factor out the common term $(n+1)$ from the numerator:
$= \frac{(n+1)[n + (n+2)]}{2}$
Simplify the term inside the square brackets:
$= \frac{(n+1)[n + n + 2]}{2}$
$= \frac{(n+1)(2n + 2)}{2}$
Factor out 2 from $(2n+2)$:
$= \frac{(n+1) \times 2(n + 1)}{2}$
Cancel the 2 in the numerator and denominator:
$= (n+1)(n+1)$
$= (n+1)^2$
This shows algebraically that the sum of the $n$-th and $(n+1)$-th triangular numbers is $(n+1)^2$, which is a perfect square. The first sum $1+3=4$ corresponds to $T_1 + T_2 = (1+1)^2 = 2^2$. The second sum $3+6=9$ corresponds to $T_2 + T_3 = (2+1)^2 = 3^2$, and so on.
Pictorial Explanation:
We can visualize this by taking a triangular arrangement of dots for $T_n$ and a triangular arrangement of dots for $T_{n+1}$ and fitting them together to form a square.
Let's consider the example $T_3 + T_4 = 6 + 10 = 16 = 4^2$.
The picture for $T_4$ is a triangle with rows of 1, 2, 3, and 4 dots:
.
. .
. . .
. . . .
(Total 10 dots)
The picture for $T_3$ is a triangle with rows of 1, 2, and 3 dots:
.
. .
. . .
(Total 6 dots)
Now, take the $T_4$ triangle and keep its orientation. Take the $T_3$ triangle, rotate it 180 degrees (so its rows are 3, 2, 1), and place it next to the $T_4$ triangle such that the longest row of $T_3$ (3 dots) aligns with the second longest row of $T_4$ (3 dots), and so on.
A better way to visualize is to take the $(n+1) \times (n+1)$ square and see how it can be partitioned into $T_n$ and $T_{n+1}$.
Consider a $4 \times 4$ square (representing $4^2 = 16$ dots):
. . . .
. . . .
. . . .
. . . .
Draw a line from the top-left corner, stepping down one row and right one column at each step. This line separates the square into two triangular regions of dots.
. | . . .
. . | . .
. . . | .
. . . . |
The dots on or below this diagonal (when including the diagonal as part of the lower region) form a triangle with rows 1, 2, 3, 4. This is $T_4$ (10 dots).
.
. .
. . .
. . . .
The dots strictly above this diagonal form a triangle with rows of 3, 2, and 1 dots (reading from bottom-left to top-right within that region). This is $T_3$ (6 dots).
. . .
. .
.
So, combining the pictorial representation of $T_{n+1}$ (the dots on or below the diagonal) and $T_n$ (the dots strictly above the diagonal, just shifted/rotated) perfectly fills the $(n+1) \times (n+1)$ square. This visually shows that $T_{n+1} + T_n = (n+1)^2$.
Question 6. What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, … ? Now add 1 to each of these numbers — what numbers do you get? Why does this happen?
Answer:
The sequence of powers of 2 starting with 1 is $1, 2, 4, 8, 16, 32, \dots$ (which are $2^0, 2^1, 2^2, 2^3, 2^4, 2^5, \dots$).
When we start to add these numbers up (cumulative sums), we get the following sequence:
- Sum of the first 1 term (1): $1 = 1$
- Sum of the first 2 terms (1, 2): $1 + 2 = 3$
- Sum of the first 3 terms (1, 2, 4): $1 + 2 + 4 = 7$
- Sum of the first 4 terms (1, 2, 4, 8): $1 + 2 + 4 + 8 = 15$
- Sum of the first 5 terms (1, 2, 4, 8, 16): $1 + 2 + 4 + 8 + 16 = 31$
- Sum of the first 6 terms (1, 2, 4, 8, 16, 32): $1 + 2 + 4 + 8 + 16 + 32 = 63$
- ...and so on.
The sequence obtained by adding up powers of 2 is 1, 3, 7, 15, 31, 63, ...
Now, let's add 1 to each number in this new sequence:
- $1 + 1 = 2$
- $3 + 1 = 4$
- $7 + 1 = 8$
- $15 + 1 = 16$
- $31 + 1 = 32$
- $63 + 1 = 64$
- ...and so on.
The sequence we get when we add 1 to each of these numbers is 2, 4, 8, 16, 32, 64, ...
This is the sequence of powers of 2, starting from $2^1$ ($2^1, 2^2, 2^3, 2^4, 2^5, 2^6, \dots$).
Why does this happen?
The sum of the first $n$ powers of 2, starting from $2^0=1$, is $2^0 + 2^1 + 2^2 + \dots + 2^{n-1}$.
This sum is equal to $2^n - 1$.
$1 + 2 + 4 + \dots + 2^{n-1} = 2^n - 1$
For example:
Sum of first 1 term ($n=1$): $2^1 - 1 = 1$
Sum of first 2 terms ($n=2$): $2^2 - 1 = 3$
Sum of first 3 terms ($n=3$): $2^3 - 1 = 7$
Sum of first 4 terms ($n=4$): $2^4 - 1 = 15$
So, the sequence of cumulative sums is $2^1-1, 2^2-1, 2^3-1, 2^4-1, \dots$.
When we add 1 to each term in this sequence $(2^n - 1)$, we get:
$(2^n - 1) + 1 = 2^n$
So, the sequence becomes $2^1, 2^2, 2^3, 2^4, \dots$.
This property arises because the sum of all powers of 2 up to a certain power is always one less than the next power of 2. If you think in binary numbers, the sum $1+2+4+...+2^{n-1}$ is represented by $n$ consecutive '1' digits (e.g., $1+2+4=7$, binary 111). Adding 1 to a binary number consisting of $n$ ones results in a '1' followed by $n$ zeros (e.g., $111_2 + 1_2 = 1000_2 = 8$), which is the binary representation of $2^n$.
Question 7. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?
Answer:
The sequence of triangular numbers is 1, 3, 6, 10, 15, 21, ...
Let's perform the operation: multiply each triangular number by 6 and add 1.
- For 1: $1 \times 6 + 1 = 7$
- For 3: $3 \times 6 + 1 = 18 + 1 = 19$
- For 6: $6 \times 6 + 1 = 36 + 1 = 37$
- For 10: $10 \times 6 + 1 = 60 + 1 = 61$
- For 15: $15 \times 6 + 1 = 90 + 1 = 91$
- For 21: $21 \times 6 + 1 = 126 + 1 = 127$
- ...and so on.
The sequence we get is 7, 19, 37, 61, 91, 127, ...
This sequence is the sequence of centered hexagonal numbers, starting from the second centered hexagonal number.
Why this happens (Algebraic Explanation):
The $n$-th triangular number is given by the formula $T_n = \frac{n(n+1)}{2}$.
We are calculating $6 \times T_n + 1$. Substituting the formula for $T_n$:
$6 \times \frac{n(n+1)}{2} + 1$
Simplify the expression:
$= 3n(n+1) + 1$
$= 3n^2 + 3n + 1$
The $k$-th centered hexagonal number, $H_k$, has the formula $H_k = 3k^2 - 3k + 1$, where $k=1$ for the first term (1 dot). Let's check if our resulting sequence $3n^2 + 3n + 1$ corresponds to centered hexagonal numbers.
If we consider the $(n+1)$-th centered hexagonal number, using the formula with $k = n+1$:
$H_{n+1} = 3(n+1)^2 - 3(n+1) + 1$
$= 3(n^2 + 2n + 1) - 3n - 3 + 1$
$= 3n^2 + 6n + 3 - 3n - 3 + 1$
$= 3n^2 + 3n + 1$
This matches the formula $3n^2 + 3n + 1$ that we obtained by multiplying the $n$-th triangular number by 6 and adding 1.
So, $6 \times T_n + 1 = H_{n+1}$. The sequence $6T_1+1, 6T_2+1, 6T_3+1, \dots$ is exactly the sequence of centered hexagonal numbers $H_2, H_3, H_4, \dots$.
Pictorial Explanation:
A centered hexagonal number can be visualized as a central dot surrounded by layers of dots arranged hexagonally. The first centered hexagonal number ($H_1=1$) is just the central dot. The second ($H_2=7$) has the central dot plus a layer of 6 dots around it. The third ($H_3=19$) has the central dot plus the first layer (6) and a second layer (12). The $k$-th layer adds $6(k-1)$ dots for $k>1$. The layers added are 6, 12, 18, 24, ...
The total number of dots in the $H_{n+1}$-th centered hexagonal number (for $n \ge 1$) is 1 (the central dot) plus the dots in the first $n$ hexagonal layers. The number of dots in the layers are $6 \times 1, 6 \times 2, \dots, 6 \times n$.
So, $H_{n+1} = 1 + (6 \times 1) + (6 \times 2) + \dots + (6 \times n)$
Factor out 6 from the sum:
$H_{n+1} = 1 + 6 \times (1 + 2 + \dots + n)$
The sum in the parentheses $(1 + 2 + \dots + n)$ is the $n$-th triangular number, $T_n$.
$H_{n+1} = 1 + 6 \times T_n$
This formula gives us the pictorial explanation:
Take a single central dot (representing 1). Take 6 copies of the pictorial representation of the $n$-th triangular number ($T_n$ dots arranged in a triangle). Arrange these 6 triangles symmetrically around the central dot. The total number of dots will form the shape of the $(n+1)$-th centered hexagonal number.
For example, to show $6 \times T_2 + 1 = H_3$: $T_2=3$. Take 6 triangles of 3 dots each. Arrange them around a central dot. The total is $6 \times 3 + 1 = 19$, which forms the third centered hexagon.
This visual arrangement demonstrates why multiplying a triangular number by 6 and adding 1 results in a centered hexagonal number.
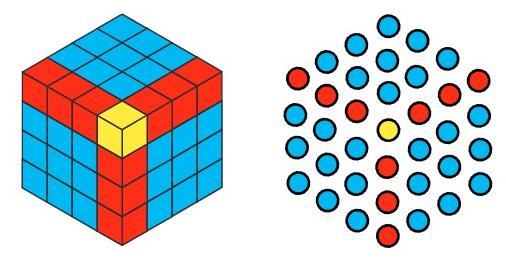
Answer:
The sequence of numbers being added up is 1, 7, 19, 37, ... These are the centered hexagonal numbers, starting from the first one ($H_1 = 1$).
Let's calculate the cumulative sums of this sequence:
- Sum of the first 1 term (1): $1 = 1$
- Sum of the first 2 terms (1, 7): $1 + 7 = 8$
- Sum of the first 3 terms (1, 7, 19): $1 + 7 + 19 = 27$
- Sum of the first 4 terms (1, 7, 19, 37): $1 + 7 + 19 + 37 = 64$
- Sum of the first 5 terms (1, 7, 19, 37, 61): $1 + 7 + 19 + 37 + 61 = 125$
- ...and so on.
The sequence we get is 1, 8, 27, 64, 125, ...
This is the sequence of cube numbers ($1^3, 2^3, 3^3, 4^3, 5^3, \dots$).
Why this happens (Pictorial Explanation using a Cube):
The terms in the sequence 1, 7, 19, 37, ... can be viewed as the number of unit cubes required to build successive layers or shells around a central unit cube, forming larger and larger cubes.
- The first term, 1, represents the central unit cube. This forms a $1 \times 1 \times 1$ cube, containing $1^3 = 1$ unit cube.
- The second term, 7, represents the number of unit cubes needed to add around the central $1 \times 1 \times 1$ cube to form a $2 \times 2 \times 2$ cube. A $2 \times 2 \times 2$ cube contains $2^3 = 8$ unit cubes. The number of cubes added is $8 - 1 = 7$. When you add these 7 cubes around the first one, you form a $2 \times 2 \times 2$ cube (total $1+7=8$).
- The third term, 19, represents the number of unit cubes needed to add around the $2 \times 2 \times 2$ cube to form a $3 \times 3 \times 3$ cube. A $3 \times 3 \times 3$ cube contains $3^3 = 27$ unit cubes. The number of cubes added is $27 - 8 = 19$. When you add these 19 cubes around the $2 \times 2 \times 2$ cube, you form a $3 \times 3 \times 3$ cube (total $8+19=27$).
- The fourth term, 37, represents the number of unit cubes needed to add around the $3 \times 3 \times 3$ cube to form a $4 \times 4 \times 4$ cube. A $4 \times 4 \times 4$ cube contains $4^3 = 64$ unit cubes. The number of cubes added is $64 - 27 = 37$. When you add these 37 cubes around the $3 \times 3 \times 3$ cube, you form a $4 \times 4 \times 4$ cube (total $27+37=64$).
The picture shows this process for building up to a $3 \times 3 \times 3$ cube. It illustrates how the numbers 1, 7, and 19 are the sizes of successive layers added. When you cumulatively add these layers ($1$, $1+7$, $1+7+19$), you are counting the total number of unit cubes in the resulting structure, which is always a perfect cube ($1^3, 2^3, 3^3$).
In general, the sum of the first $n$ centered hexagonal numbers is the total number of cubes in an $n \times n \times n$ cube, which is $n^3$.
| Table 1 Examples of number sequences | |
|---|---|
| 1, 1, 1, 1, 1, 1, 1, ... | (All 1’s) |
| 1, 2, 3, 4, 5, 6, 7, ... | (Counting numbers) |
| 1, 3, 5, 7, 9, 11, 13, ... | (Odd numbers) |
| 2, 4, 6, 8, 10, 12, 14, ... | (Even numbers) |
| 1, 3, 6, 10, 15, 21, 28, ... | (Triangular numbers) |
| 1, 4, 9, 16, 25, 36, 49, ... | (Squares) |
| 1, 8, 27, 64, 125, 216, ... | (Cubes) |
| 1, 2, 3, 5, 8, 13, 21, ... | (Virahānka numbers) |
| 1, 2, 4, 8, 16, 32, 64, ... | (Powers of 2) |
| 1, 3, 9, 27, 81, 243, 729, ... | (Powers of 3) |
Answer:
There are many interesting patterns and relationships among these sequences. Here are a couple that can be explained pictorially or otherwise:
Pattern 1: Relationship between Counting Numbers and Triangular Numbers
The sequence of Counting numbers is 1, 2, 3, 4, ...
The sequence of Triangular numbers is 1, 3, 6, 10, ...
As noted in a previous question, the $n$-th triangular number is the sum of the first $n$ counting numbers: $T_n = 1 + 2 + \dots + n$.
Explanation (Pictorial):
Consider two copies of the picture representing the $n$-th triangular number, $T_n$. For example, let's take $n=4$, where $T_4 = 1+2+3+4=10$. The picture is a triangle with rows of 1, 2, 3, and 4 dots:
.
. .
. . .
. . . .
Now, take a second copy of this triangle and rotate it 180 degrees (flip it upside down). Its rows will be 4, 3, 2, 1:
. . . .
. . .
. .
.
If you place the second (rotated) triangle next to the first triangle, aligning their longest sides, they form a rectangle.
. . . . .
. . . . .
. . . . .
. . . . .
This rectangle has $n=4$ rows and $(n+1)=5$ columns. The total number of dots in this rectangle is $4 \times 5 = 20$. Since this rectangle is formed by two copies of the $T_4$ triangle, the number of dots in one $T_4$ triangle is half the number of dots in the rectangle.
Total dots = $T_n + T_n = 2 T_n$
... (i)
Total dots = $n \times (n+1)$
... (ii)
Equating (i) and (ii):
$2 T_n = n(n+1)$
Dividing by 2:
$T_n = \frac{n(n+1)}{2}$
This pictorial method shows why the sum of the first $n$ counting numbers is the $n$-th triangular number, and it also gives a visual explanation for the formula $\frac{n(n+1)}{2}$.
Pattern 2: Relationship between Consecutive Square Numbers and Odd Numbers
The sequence of Square numbers is 1, 4, 9, 16, 25, ...
The sequence of Odd numbers is 1, 3, 5, 7, 9, ...
Look at the difference between consecutive square numbers:
- $4 - 1 = 3$ (The 2nd odd number)
- $9 - 4 = 5$ (The 3rd odd number)
- $16 - 9 = 7$ (The 4th odd number)
- $25 - 16 = 9$ (The 5th odd number)
- ...and so on.
It appears that the difference between the $n$-th square number ($n^2$) and the $(n-1)$-th square number ($(n-1)^2$) is the $n$-th odd number ($2n-1$). In other words, $n^2 = (n-1)^2 + (2n-1)$.
Explanation (Pictorial):
Consider an $(n-1) \times (n-1)$ square of dots. This square contains $(n-1)^2$ dots.
For example, a $3 \times 3$ square ($n-1=3$, $n=4$):
. . .
. . .
. . .
Now, to make it an $n \times n$ square (a $4 \times 4$ square in this example), we need to add a layer of dots around two adjacent sides of the $(n-1) \times (n-1)$ square.
Imagine adding a row of $n$ dots along the bottom and a column of $n-1$ dots along the right side (excluding the corner dot, which is part of the bottom row).
For the $3 \times 3$ square becoming a $4 \times 4$ square ($n-1=3, n=4$):
. . . | .
. . . | .
. . . | .
- - - - -
. . . .
The dots we added form an L-shape (or a gnomon). The number of dots in the L-shape is $n$ (bottom row) + $(n-1)$ (right column) = $2n-1$. This is the $n$-th odd number.
So, adding the $n$-th odd number of dots (in an L-shape) to the $(n-1) \times (n-1)$ square (which has $(n-1)^2$ dots) results in an $n \times n$ square (which has $n^2$ dots).
$(n-1)^2$ (previous square) + $(2n-1)$ ($n$-th odd number) = $n^2$ (current square)
This pictorial representation explains why adding consecutive odd numbers starting from 1 results in square numbers, and it also shows how each square is built from the previous one by adding the next odd number.
Figure it Out (Page 11)
| Table 3 Examples of Shape Sequences | |
|---|---|
| Regular Polygons | .jpg)
|
| Complete Graphs | .jpg)
|
| Stacked Squares | .jpg)
|
| Stacked Triangles | .jpg)
|
| Koch Snowflake | .jpg)
|
Question 1. Can you recognise the pattern in each of the sequences in Table 3?
Answer:
Yes, the pattern in each of the shape sequences in Table 3 can be recognized.
1. Regular Polygons:
Pattern: This sequence shows a progression of regular polygons, starting with the simplest ones. Each subsequent shape is a regular polygon with one more side than the previous shape. The sequence is: Triangle (3 sides), Square (4 sides), Pentagon (5 sides), Hexagon (6 sides).
2. Complete Graphs:
Pattern: This sequence shows graphs where each point (vertex) is connected by a line (edge) to every other point. The pattern increases the number of points by one at each step and adds all possible lines between them. The number of points in the sequence is 1, 2, 3, 4. The number of lines added at each step are 0, 1, 2, 3, ... respectively (starting from 1 point). The total number of lines is 0, 1, 3, 6, which are triangular numbers $T_{n-1}$ where $n$ is the number of points.
3. Stacked Squares:
Pattern: This sequence shows squares made of smaller unit squares, built up in layers. The pattern is forming larger and larger squares by adding layers. The number of small squares in each picture is 1, 4, 9, 16, which are the square numbers ($1^2, 2^2, 3^2, 4^2$). Each picture represents an $n \times n$ square of unit squares.
4. Stacked Triangles:
Pattern: This sequence shows triangles made of smaller unit triangles, built up in layers. The pattern is forming larger and larger triangles by adding rows. The number of small triangles in each picture is 1, 3, 6, 10, which are the triangular numbers ($T_1, T_2, T_3, T_4$). Each picture represents a triangle formed by summing the first $n$ counting numbers.
5. Koch Snowflake:
Pattern: This sequence illustrates the first few steps in the construction of a fractal called the Koch snowflake. Starting from an equilateral triangle, in each subsequent step, the middle third of every line segment in the perimeter is removed and replaced by two segments that form two sides of a smaller equilateral triangle, pointing outwards. This process is repeated infinitely to create the final fractal shape.
Question 2. Try and redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.
Answer:
As an AI, I cannot draw the shapes in your notebook, but I can describe how to redraw them and what the next shape would be for each sequence. I will also describe the rule for forming each sequence.
1. Regular Polygons:
Rule/Pattern: This sequence shows regular polygons where each subsequent shape has one more side than the previous one. It starts with a 3-sided polygon (triangle), then a 4-sided polygon (square), a 5-sided polygon (pentagon), and a 6-sided polygon (hexagon).
Drawing the next shape: Yes, you can draw the next shape. Following the pattern, the next regular polygon should have 7 sides.
Description of the next shape: The next shape is a regular heptagon, a polygon with 7 equal sides and 7 equal angles.
2. Complete Graphs:
Rule/Pattern: This sequence shows a set of points (vertices) where every point is connected by a line segment (edge) to every other point. The pattern is to add one new point at each step and then add all possible connecting lines between this new point and all existing points, as well as ensure all original points are connected to each other.
Drawing the next shape: Yes, you can draw the next shape, but it gets more complex. The number of points increases by one each time. The sequence has 1, 2, 3, 4 points.
Description of the next shape: The next shape will have 5 points. You should draw 5 points and then draw a line connecting every single point to every other point. For example, if you label the points A, B, C, D, E, you would draw lines AB, AC, AD, AE, BC, BD, BE, CD, CE, and DE. The number of lines will be the sum of the number of points added at each step: $0+1+2+3+4=10$, which is the triangular number $T_{5-1}=T_4$. More generally, a complete graph with $n$ vertices has $\frac{n(n-1)}{2}$ edges. For $n=5$, this is $\frac{5(4)}{2}=10$ edges.
3. Stacked Squares:
Rule/Pattern: This sequence shows squares made up of smaller unit squares. The pattern is forming larger squares by increasing the side length by one unit at each step. The shapes are a $1 \times 1$ square, a $2 \times 2$ square, a $3 \times 3$ square, and a $4 \times 4$ square, containing $1^2=1$, $2^2=4$, $3^2=9$, $4^2=16$ unit squares, respectively.
Drawing the next shape: Yes, you can draw the next shape.
Description of the next shape: The next shape will be a $5 \times 5$ square made up of $5^2 = 25$ smaller unit squares.
4. Stacked Triangles:
Rule/Pattern: This sequence shows triangles made up of smaller unit triangles, arranged in rows. The pattern is forming larger triangles by adding a new row of unit triangles at the base, where the number of triangles in the new row is one more than the previous row. The number of unit triangles in each picture is 1, 3, 6, 10, which are the triangular numbers ($T_1, T_2, T_3, T_4$). The $n$-th shape is a triangle formed by stacking rows of 1, 2, ..., up to $n$ unit triangles.
Drawing the next shape: Yes, you can draw the next shape.
Description of the next shape: The next shape will be a triangle formed by adding a 5th row of unit triangles to the base of the triangle with 4 rows. The total number of unit triangles will be $T_5 = 1 + 2 + 3 + 4 + 5 = 15$. The picture will show 5 rows with 1, 2, 3, 4, and 5 unit triangles, respectively, forming a larger triangle.
5. Koch Snowflake:
Rule/Pattern: This sequence is generated by an iterative process. Starting with an equilateral triangle, each step involves taking every straight line segment and replacing its middle third with two segments of equal length, forming an outward-pointing equilateral triangle. This process is applied simultaneously to all segments in the shape at each step.
Drawing the next shape: You can draw the next step (the 5th shape in the sequence), but drawing subsequent steps becomes increasingly difficult and the theoretical "final" shape (the true Koch snowflake) is impossible to draw perfectly because it has infinite detail.
Description of the next shape: To get the next shape, take every straight line segment in the 4th shape and apply the rule: divide the segment into three equal parts, remove the middle part, and draw two new segments forming an equilateral triangle on that removed part. This will significantly increase the number of sides and make the shape's boundary much more complex and bumpy.
Figure it Out (Page 11 - 12)
Question 1. Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Answer:
The sequence of Regular Polygons shown is Triangle, Square, Pentagon, Hexagon, ...
Let's count the number of sides for each shape in the sequence:
- Triangle: 3 sides
- Square: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- ... and so on.
The number sequence we get for the sides is 3, 4, 5, 6, ...
Now, let's count the number of corners (vertices) for each shape in the sequence:
- Triangle: 3 corners
- Square: 4 corners
- Pentagon: 5 corners
- Hexagon: 6 corners
- ... and so on.
The number sequence we get for the corners is also 3, 4, 5, 6, ...
Yes, we get the same number sequence for both the number of sides and the number of corners in the sequence of Regular Polygons.
Explanation:
This happens because, by definition, a polygon is a closed two-dimensional shape made up of straight line segments joined end to end. Each point where two line segments meet is called a vertex (or corner), and each line segment between two vertices is called a side.
In any closed polygon, every side connects exactly two vertices, and every vertex is the meeting point of exactly two sides. There is a one-to-one correspondence between the sides and the vertices. If a polygon has $n$ sides, it must connect these sides at $n$ distinct vertices. Conversely, if a polygon has $n$ vertices, these vertices must be connected by $n$ sides to form a closed shape.
Therefore, for any polygon (regular or irregular), the number of sides is always equal to the number of corners.
Question 2. Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get? Can you explain why?
Answer:
The sequence of Complete Graphs shows graphs with an increasing number of points (vertices).
Let's count the number of lines (edges) in each shape:
- Graph with 1 point: 0 lines
- Graph with 2 points: 1 line
- Graph with 3 points: 3 lines
- Graph with 4 points: 6 lines
- ... and so on.
The number sequence we get for the lines is 0, 1, 3, 6, ...
Explanation:
A complete graph is defined by having a line connecting every pair of distinct points. Let $n$ be the number of points (vertices) in the graph.
Consider any single point in the graph. It needs to be connected to every other point. Since there are $n$ total points, this single point needs to be connected to $n-1$ other points.
If we do this for all $n$ points, we might think the total number of lines is $n \times (n-1)$. However, this method counts each line twice. For instance, the line connecting point A to point B is counted when we consider the connections from point A, and it is counted again when we consider the connections from point B.
To get the actual number of unique lines, we must divide the product by 2.
The number of lines in a complete graph with $n$ points is given by the formula: $\frac{n \times (n-1)}{2}$.
Let's check the formula with the number of points in the given sequence:
- For $n=1$: $\frac{1 \times (1-1)}{2} = \frac{1 \times 0}{2} = 0$
- For $n=2$: $\frac{2 \times (2-1)}{2} = \frac{2 \times 1}{2} = 1$
- For $n=3$: $\frac{3 \times (3-1)}{2} = \frac{3 \times 2}{2} = 3$
- For $n=4$: $\frac{4 \times (4-1)}{2} = \frac{4 \times 3}{2} = \frac{12}{2} = 6$
The sequence 0, 1, 3, 6, ... is the sequence of triangular numbers, but starting from the "0-th" triangular number (0), then the 1st (1), 2nd (3), 3rd (6), and so on. The $n$-th term in the sequence of lines (starting with $n=1$ for the 1-point graph) is the $(n-1)$-th triangular number, $T_{n-1} = \frac{(n-1)((n-1)+1)}{2} = \frac{(n-1)n}{2}$.
Question 3. How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?
Answer:
The sequence of Stacked Squares shows shapes formed by arranging smaller unit squares into larger square shapes.
Let's count the number of little squares in each shape:
- The first shape is a $1 \times 1$ square: It has 1 little square.
- The second shape is a $2 \times 2$ square: It has $2 \times 2 = 4$ little squares.
- The third shape is a $3 \times 3$ square: It has $3 \times 3 = 9$ little squares.
- The fourth shape is a $4 \times 4$ square: It has $4 \times 4 = 16$ little squares.
- ... and so on.
The number sequence we get is 1, 4, 9, 16, ...
This is the sequence of square numbers.
Explanation:
This happens because the shapes in the sequence are constructed as perfect squares made up of smaller unit squares. The $n$-th shape in the sequence is an $n \times n$ square.
To find the total number of little squares in an $n \times n$ square, we multiply the number of squares along one side (which is $n$) by the number of squares along an adjacent side (which is also $n$).
Total number of little squares = Number of rows $\times$ Number of columns
Total number of little squares = $n \times n = n^2$
Thus, the number of little squares in the $n$-th shape of the Stacked Squares sequence is $n^2$, which directly generates the sequence of square numbers: $1^2=1, 2^2=4, 3^2=9, 4^2=16$, etc.
Question 4. How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why?
(Hint: In each shape in the sequence, how many triangles are there in each row?)
Answer:
The sequence of Stacked Triangles shows shapes formed by arranging smaller unit triangles into larger triangular shapes by adding rows.
Let's count the number of little triangles in each shape, following the hint about the number of triangles in each row:
- The first shape has 1 row with 1 triangle. Total: 1.
- The second shape has 2 rows: the top row has 1 triangle, the bottom row has 2 triangles. Total: $1 + 2 = 3$.
- The third shape has 3 rows: 1 in the top row, 2 in the second row, and 3 in the bottom row. Total: $1 + 2 + 3 = 6$.
- The fourth shape has 4 rows: 1, 2, 3, and 4 triangles in the rows from top to bottom. Total: $1 + 2 + 3 + 4 = 10$.
- ... and so on.
The number sequence we get is 1, 3, 6, 10, ...
This is the sequence of triangular numbers.
Explanation:
This happens because of how each subsequent shape in the sequence is constructed. The pattern is to build the $n$-th triangle by adding a new row containing $n$ unit triangles to the bottom of the $(n-1)$-th triangle (which contained $1+2+...+(n-1)$ unit triangles).
The number of unit triangles in the $n$-th shape is the sum of the number of triangles in each of its rows. According to the construction, the rows contain 1, 2, 3, ..., up to $n$ triangles.
So, the total number of triangles in the $n$-th shape is the sum: $1 + 2 + 3 + \dots + n$.
This sum is the definition of the $n$-th triangular number, denoted as $T_n$.
Number of triangles in $n$-th shape = $T_n = \sum_{i=1}^{n} i = \frac{n(n+1)}{2}$
Thus, the number of little triangles in the shapes of the Stacked Triangles sequence directly generates the sequence of triangular numbers: $T_1=1, T_2=3, T_3=6, T_4=10$, etc.
Question 5. To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘—’ by a ‘speed bump’ __⋀__ . As one does this more and more times, the changes become tinier and tinier with very very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence? (The answer is 3, 12, 48, ..., i.e. 3 times Powers of 4; this sequence is not shown in Table 1)
Answer:
The Koch Snowflake sequence starts with an initial shape and applies a specific transformation rule repeatedly.
The Initial Shape (Step 0):
The sequence begins with an equilateral triangle. A triangle has 3 line segments (sides).
The Transformation Rule:
For each line segment in the current shape, the middle third is removed, and two new segments are added to form two sides of a smaller equilateral triangle. This effectively replaces one line segment with four smaller line segments.
1 line segment $\to$ 4 line segments
Counting the Total Line Segments at Each Step:
- Step 0: Start with the initial triangle. Number of segments = 3.
- Step 1: Each of the 3 segments from Step 0 is replaced by 4 segments. Total segments = $3 \times 4 = 12$.
- Step 2: Each of the 12 segments from Step 1 is replaced by 4 segments. Total segments = $12 \times 4 = 48$.
- Step 3: Each of the 48 segments from Step 2 is replaced by 4 segments. Total segments = $48 \times 4 = 192$.
- ... and so on.
The number of segments is multiplied by 4 at each step.
The Corresponding Number Sequence:
The sequence of the total number of line segments in each shape is: 3, 12, 48, 192, ...
Explanation:
This sequence is indeed generated by starting with 3 and repeatedly multiplying by 4. This can be expressed as 3 times the powers of 4:
- Step 0: $3 = 3 \times 1 = 3 \times 4^0$
- Step 1: $12 = 3 \times 4 = 3 \times 4^1$
- Step 2: $48 = 3 \times 16 = 3 \times 4^2$
- Step 3: $192 = 3 \times 64 = 3 \times 4^3$
- ...
- Step $k$: $3 \times 4^k$
The reason this happens is directly because of the transformation rule: every time you perform the iteration (move to the next step in the sequence), each existing line segment is replaced by exactly four new, smaller line segments. Since you start with 3 segments and each one independently quadruples, the total number of segments quadruples at every step.

